While I am preparing my poster corner presentation this evening, I tried a few simulations to see if I can give more intuitive explanations rather than just stating the “facts”.
First I tried with two normal distributions with very different variance, the test result is not significant. I then tried with one normal and the other being heavy tailed exponential, and I got a significant result. I increase the sample size from 100 to 1000, the significance now is clear.
The Misconception
It is commonly perceived that nonparametric tests are “assumption-free” or at least free from the homogeneity of variance assumption. This is not entirely accurate and leads to confusion.
What Nonparametric Tests Actually Test
Most common nonparametric tests (Mann-Whitney U, Wilcoxon signed-rank, Kruskal-Wallis) technically test whether samples come from identical distributions, not just whether they have equal central tendencies. The null hypothesis is typically:
\(H_0\): The distributions in the compared groups are identical
If the distributions have different shapes or spreads (including different variances), rejecting this null hypothesis doesn’t necessarily mean the central tendencies differ.
The Role of Homogeneity of Variance
When we use nonparametric tests specifically to test for differences in central tendencies (medians or means), we are implicitly assuming that the distributions have the same shape and spread. Without this assumption, a significant result could indicate:
Different central tendencies or medians or means
Different variances
Different shapes
Some combination of these differences
Example: Mann-Whitney U Test
If we reject the null hypothesis in a Mann-Whitney U test between two groups with different variances, we cannot confidently conclude that the medians differ. The significant result might be due to the difference in spread rather than central location. This is actually also not something I know by heart. Therefore, I conducted a small simulation study to understand that.
Implications for Practitioners
A significant test result doesn’t necessarily mean central tendencies / medians differ.
When variances are unequal, the test may be detecting this inequality rather than a difference in medians.
Visual inspection of the data (histograms, boxplots) is essential for proper interpretation.
A Simple Simulation
Note that I used genAI to generate python code instead of writing R code by myself, as a way of familiarize myself more with python programming. I simply states what I want to do and mygenAssist produced something as expected with a few modifications.
import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsfrom scipy import statsimport math# Set random seed for reproducibilitynp.random.seed(42)n =1000# Sample size# Scenario 1: Two normal distributions with same median/mean but different variancesnorm1 = np.random.normal(0, 1, n) # Normal with mean=0, sd=1norm2 = np.random.normal(0, 3, n) # Normal with mean=0, sd=3# Scenario 2: Normal vs. shifted exponentialexp_scale =2exp_shift =-2norm3 = np.random.normal(0, 1, n) # Normal with mean=0, sd=1exp1 = np.random.exponential(exp_scale, n) + exp_shift # Shifted exponential# Calculate theoretical and empirical statisticsprint("=== Scenario 1: Two Normal Distributions ===")print(f"Normal 1 - Mean: {np.mean(norm1):.4f}, Median: {np.median(norm1):.4f}, Variance: {np.var(norm1):.4f}")print(f"Normal 2 - Mean: {np.mean(norm2):.4f}, Median: {np.median(norm2):.4f}, Variance: {np.var(norm2):.4f}")print("\n=== Scenario 2: Normal vs. 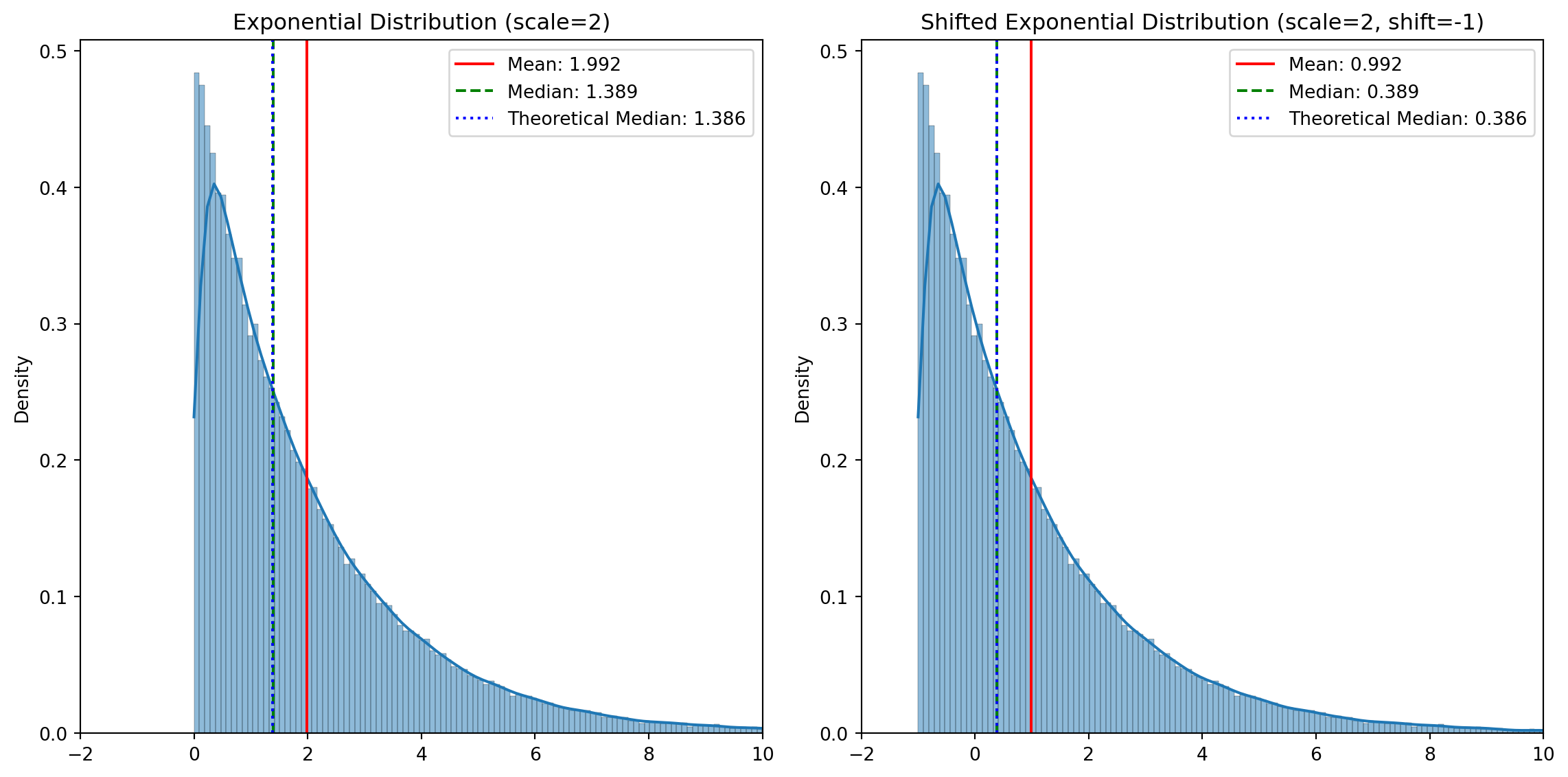Shifted Exponential ===")print(f"Normal - Mean: {np.mean(norm3):.4f}, Median: {np.median(norm3):.4f}")print(f"Shifted Exp - Mean: {np.mean(exp1):.4f}, Median: {np.median(exp1):.4f}")print(f"Shifted Exp - Theoretical Mean: {exp_scale + exp_shift}, Theoretical Median: {exp_scale * math.log(2) + exp_shift:.4f}")# Perform Mann-Whitney U testsu_stat1, p_value1 = stats.mannwhitneyu(norm1, norm2, alternative='two-sided')u_stat2, p_value2 = stats.mannwhitneyu(norm3, exp1, alternative='two-sided')# Perform Welch's t-tests (t-test with unequal variances)t_stat1, t_p_value1 = stats.ttest_ind(norm1, norm2, equal_var=False)t_stat2, t_p_value2 = stats.ttest_ind(norm3, exp1, equal_var=False)print("\n=== Statistical Test Results ===")print("Scenario 1 (Two Normals with Different Variances):")print(f" Mann-Whitney U Test - U: {u_stat1}, p-value: {p_value1:.6f}, Significant: {p_value1 <0.05}")print(f" Welch's t-test - t: {t_stat1:.4f}, p-value: {t_p_value1:.6f}, Significant: {t_p_value1 <0.05}")print("\nScenario 2 (Normal vs. Shifted Exponential):")print(f" Mann-Whitney U Test - U: {u_stat2}, p-value: {p_value2:.6f}, Significant: {p_value2 <0.05}")print(f" Welch's t-test - t: {t_stat2:.4f}, p-value: {t_p_value2:.6f}, Significant: {t_p_value2 <0.05}")# Visualize distributionsplt.figure(figsize=(12, 10))# Scenario 1: Two normal distributionsplt.subplot(2, 2, 1)sns.histplot(norm1, kde=True, stat="density", label="Normal(0,1)")sns.histplot(norm2, kde=True, stat="density", label="Normal(0,3)")plt.axvline(x=np.median(norm1), color='blue', linestyle='--', label=f'Median Normal(0,1)')plt.axvline(x=np.median(norm2), color='orange', linestyle='--', label=f'Median Normal(0,3)')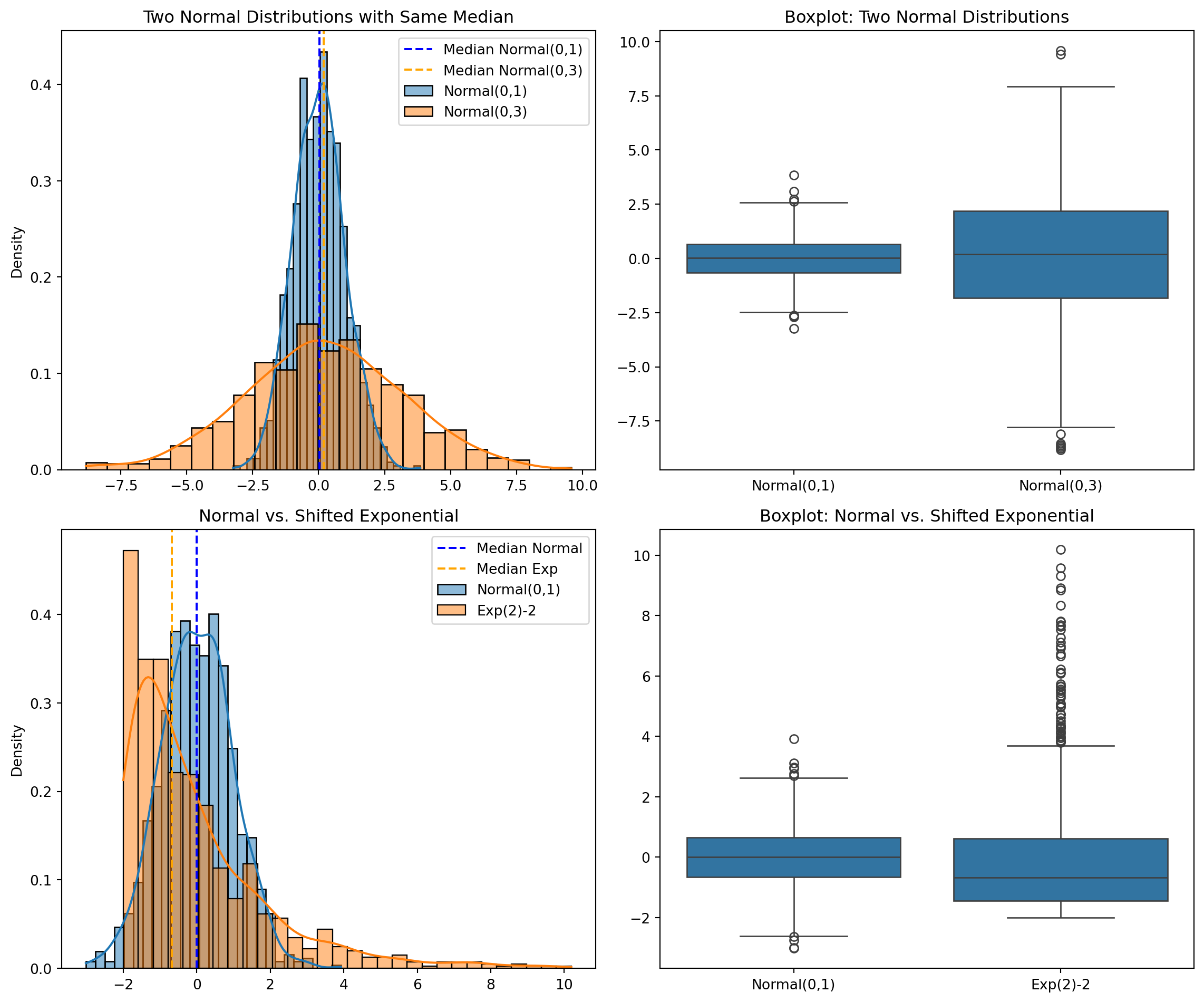plt.title('Two Normal Distributions with Same Median')plt.legend()plt.subplot(2, 2, 2)data1 = np.concatenate([norm1, norm2])groups1 = ['Normal(0,1)']*n + ['Normal(0,3)']*nsns.boxplot(x=groups1, y=data1)plt.title('Boxplot: Two Normal Distributions')# Scenario 2: Normal vs. shifted exponentialplt.subplot(2, 2, 3)sns.histplot(norm3, kde=True, stat="density", label="Normal(0,1)")sns.histplot(exp1, kde=True, stat="density", label=f"Exp({exp_scale}){exp_shift}")plt.axvline(x=np.median(norm3), color='blue', linestyle='--', label=f'Median Normal')plt.axvline(x=np.median(exp1), color='orange', linestyle='--', label=f'Median Exp')plt.title('Normal vs. Shifted Exponential')plt.legend()plt.subplot(2, 2, 4)data2 = np.concatenate([norm3, exp1])groups2 = ['Normal(0,1)']*n + [f'Exp({exp_scale}){exp_shift}']*nsns.boxplot(x=groups2, y=data2)plt.title('Boxplot: Normal vs. Shifted Exponential')plt.tight_layout()plt.show()# Rank analysis to understand whyprint("\n=== Rank Analysis ===")# Combine and rank all values for scenario 1combined1 = np.concatenate([norm1, norm2])ranks1 = stats.rankdata(combined1)rank_norm1 = ranks1[:n]rank_norm2 = ranks1[n:]print(f"Scenario 1 - Mean rank Normal(0,1): {np.mean(rank_norm1):.2f}")print(f"Scenario 1 - Mean rank Normal(0,3): {np.mean(rank_norm2):.2f}")# Combine and rank all values for scenario 2combined2 = np.concatenate([norm3, exp1])ranks2 = stats.rankdata(combined2)rank_norm3 = ranks2[:n]rank_exp1 = ranks2[n:]print(f"Scenario 2 - Mean rank Normal(0,1): {np.mean(rank_norm3):.2f}")print(f"Scenario 2 - Mean rank Exp({exp_scale}){exp_shift}: {np.mean(rank_exp1):.2f}")
=== Scenario 1: Two Normal Distributions ===
Normal 1 - Mean: 0.0193, Median: 0.0253, Variance: 0.9579
Normal 2 - Mean: 0.2125, Median: 0.1892, Variance: 8.9453
=== Scenario 2: Normal vs. Shifted Exponential ===
Normal - Mean: 0.0058, Median: -0.0003
Shifted Exp - Mean: -0.0653, Median: -0.6785
Shifted Exp - Theoretical Mean: 0, Theoretical Median: -0.6137
=== Statistical Test Results ===
Scenario 1 (Two Normals with Different Variances):
Mann-Whitney U Test - U: 474548.0, p-value: 0.048727, Significant: True
Welch's t-test - t: -1.9402, p-value: 0.052586, Significant: False
Scenario 2 (Normal vs. Shifted Exponential):
Mann-Whitney U Test - U: 605348.0, p-value: 0.000000, Significant: True
Welch's t-test - t: 1.0286, p-value: 0.303827, Significant: False
=== Rank Analysis ===
Scenario 1 - Mean rank Normal(0,1): 975.05
Scenario 1 - Mean rank Normal(0,3): 1025.95
Scenario 2 - Mean rank Normal(0,1): 1105.85
Scenario 2 - Mean rank Exp(2)-2: 895.15
Testing of python functions
As I am not very familiar with the python functions, I tried to understand the parameter settings by simulating samples from the exponential distribution.
The probability density function (PDF) of the exponential distribution is given by: \[ f(x; \lambda) = \lambda e^{-\lambda x}, \quad x \geq 0 \] ,where $ $ is the rate parameter.
In NumPy, the scale parameter is actually $ $.
import numpy as npimport matplotlib.pyplot as pltimport seaborn as snsimport math# Set random seed for reproducibilitynp.random.seed(42)# Parametersscale =2# Scale parameter for exponential distribution (can be changed)shift =-1# Shift amountn =100000# Sample size# Generate samplesexp_sample = np.random.exponential(scale, n)shifted_sample = exp_sample + shift # Shift the distribution# Calculate empirical statisticsexp_mean = np.mean(exp_sample)exp_median = np.median(exp_sample)shifted_mean = np.mean(shifted_sample)shifted_median = np.median(shifted_sample)# Calculate theoretical valuestheoretical_exp_mean = scale # Mean of Exp(scale) is scaletheoretical_exp_median = scale * math.log(2) # Median of Exp(scale) is scale*ln(2)theoretical_shifted_mean = theoretical_exp_mean + shift # Mean after shiftingtheoretical_shifted_median = theoretical_exp_median + shift # Median after shifting# Print resultsprint(f"=== Original Exponential Distribution (scale={scale}) ===")print(f"Theoretical Mean: {theoretical_exp_mean}")print(f"Empirical Mean: {exp_mean:.6f}")print(f"Theoretical Median: {theoretical_exp_median:.6f}")print(f"Empirical Median: {exp_median:.6f}")print(f"\n=== Shifted Exponential Distribution (scale={scale}, shift={shift}) ===")print(f"Theoretical Mean: {theoretical_shifted_mean}")print(f"Empirical Mean: {shifted_mean:.6f}")print(f"Theoretical Median: {theoretical_shifted_median:.6f}")print(f"Empirical Median: {shifted_median:.6f}")# Visualize both distributionsplt.figure(figsize=(12, 6))# Original exponential distributionplt.subplot(1, 2, 1)sns.histplot(exp_sample, kde=True, stat="density")plt.axvline(x=exp_mean, color='r', linestyle='-', label=f'Mean: {exp_mean:.3f}')plt.axvline(x=exp_median, color='g', linestyle='--', label=f'Median: {exp_median:.3f}')plt.axvline(x=theoretical_exp_median, color='b', linestyle=':', label=f'Theoretical Median: {theoretical_exp_median:.3f}')plt.title(f'Exponential Distribution (scale={scale})')plt.xlim(-2, max(10, scale*5))plt.legend()# Shifted exponential distributionplt.subplot(1, 2, 2)sns.histplot(shifted_sample, kde=True, stat="density")plt.axvline(x=shifted_mean, color='r', linestyle='-', label=f'Mean: {shifted_mean:.3f}')plt.axvline(x=shifted_median, color='g', linestyle='--', label=f'Median: {shifted_median:.3f}')plt.axvline(x=theoretical_shifted_median, color='b', linestyle=':', label=f'Theoretical Median: {theoretical_shifted_median:.3f}')plt.title(f'Shifted Exponential Distribution (scale={scale}, shift={shift})')plt.xlim(-2, max(10, scale*5))plt.legend()plt.tight_layout()plt.show()# Let's also verify with a different approach using percentileprint("\n=== Verification using percentile function ===")print(f"50th percentile (median) of original: {np.percentile(exp_sample, 50):.6f}")print(f"50th percentile (median) of shifted: {np.percentile(shifted_sample, 50):.6f}")# Demonstrate relationship between scale and medianscales = [0.5, 1, 2, 3, 5]print("\n=== Relationship between scale and median ===")print("Scale\tTheoretical Median\tEmpirical Median")for s in scales: sample = np.random.exponential(s, n) theo_median = s * math.log(2) emp_median = np.median(sample)print(f"{s}\t{theo_median:.6f}\t\t{emp_median:.6f}")
=== Original Exponential Distribution (scale=2) ===
Theoretical Mean: 2
Empirical Mean: 1.991940
Theoretical Median: 1.386294
Empirical Median: 1.388815
=== Shifted Exponential Distribution (scale=2, shift=-1) ===
Theoretical Mean: 1
Empirical Mean: 0.991940
Theoretical Median: 0.386294
Empirical Median: 0.388815
=== Verification using percentile function ===
50th percentile (median) of original: 1.388815
50th percentile (median) of shifted: 0.388815
=== Relationship between scale and median ===
Scale Theoretical Median Empirical Median
0.5 0.346574 0.348458
1 0.693147 0.695421
2 1.386294 1.378151
3 2.079442 2.098406
5 3.465736 3.446745
